Διάσημες καμπύλες
Δύο από τα πιο γνωστά μαθηματικά προβλήματα όλων των εποχών είναι η - με κανόνα και διαβήτη- τριχοτόμηση της γωνίας και ο τετραγωνισμός του κύκλου. Μαζί με το διπλασιασμό του κύβου (Δήλιο πρόβλημα), αποτελούν τα τρία κλασικά προβλήματα της αρχαιότητας, το "άλυτο" των οποίων αντιμετωπίσθηκε οριστικά με τη θεωρία του Galois (1832).
Η επίλυση των προβλημάτων αυτών δεν είναι λοιπόν δυνατή με χρήση ευθείας και κύκλου. Είναι όμως δυνατή με τη βοήθεια καμπύλων με εξισώσεις ανωτέρου του 2ου βαθμού, όπως είναι η κισσοειδής του Διοκλή για το Δήλιο πρόβλημα, η κογχοειδής καμπύλη του Νικομήδη για την τριχοτόμηση της γωνίας και η υπερβατική καμπύλη του Ρώσου μηχανικού Abdank Aba Kanowicz (1890) για τον τετραγωνισμό του κύκλου.
Οι αρχαίοι Έλληνες γεωμέτρες επινόησαν κι άλλες τέτοιες καμπύλες όπως: η τετραγωνίζουσα του Ιππία και η ελικοειδής του Αρχιμήδη. Από τον 17ο αιώνα και μετά στη μελέτη καμπύλων όπως: κυκλοειδής,καρδιοειδής, νεφροειδής κ.α. αφοσιώθηκαν και οι Leibniz, Bernulli, Euler, Newton και άλλοι.
Να συμπληρώσω ότι στην αρχαία Ελληνική γεωμετρία οι καμπύλες ορίζονται με 3 τρόπους:
α) σαν τομές επιφανειών (κωνικές τομές)
β) σαν γραμμές που διαγράφονται από κίνηση ή συνδυασμό κινήσεων (σπείρα, έλικα, τετραγωνίζουσα)
γ) σαν γεωμετρικός τόπος σημείων με κοινή ιδιότητα (κύκλος, κισσοειδής)
Aς γνωρίσουμε μερικές από αυτές.
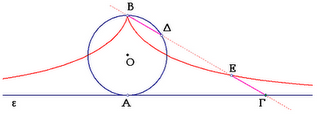
1) Κισσοειδής του Διοκλή (1ος αιώνας π.Χ.)
Σε κύκλο (Ο ,ΟΑ) φέρουμε την εφαπτομένη του ε στο σημείο Α
και έστω Β το αντιδιαμετρικό σημείο του Α .
Επί της ε παίρνουμε τυχαίο σημείο Γ και έστω Δ το σημείο
τομής της ευθείας ΒΓ με τον κύκλο .
Αν Ε είναι σημείο της ευθείας ΒΓ , τέτοιο ώστε ΓΕ = ΒΔ
, τότε καθώς το σημείο Δ κινείται επί του κύκλου , το Ε διαγράφει την λεγόμενη κισσοειδή
καμπύλη του Διοκλή (γεωμετρικός τόπος)
Η εξίσωσή της σε καρτεσιανές συντεταγμένες είναι η:
ενώ η παραμετρική της εξίσωση είναι η:2) Koγχοειδής του Νικομήδη(2ος αιώνας π.Χ.)
Μεταβλητή ευθεία ε που περνάει από την αρχή Ο καρτεσιανού συστήματος αξόνων Οxy τέμνει τη σταθερή ευθεία x = a στο σημείο Α . Πάνω στην ευθεία ε και
γύρω από το Α παίρνουμε τα σημεία Μ και Μ′ έτσι, ώστε: ΑΜ = ΑΜ′ = b .
Ο γεωμετρικός τόπος των σημείων Μ και Μ′ είναι η λεγόμενη κογχοειδής καμπύλη, με εξίσωση σε καρτεσιανές συντεταγμένες:
και σχήμα:
Όργανο για την κατασκευή της κογχοειδής καμπύλης
3) Ελικοειδής του Αρχιμήδη (σπείρα , 3ος αιώνας π.Χ.)
Θεωρούμε την ημιευθεία ΟΒ, η οποία μπορεί να περιστρέφεται του σταθερού σημείου Ο. Πάνω σε αυτήν κινείται σημείο Ρ με σταθερή ταχύτητα από το Ο προς το Β. Ο γεωμετρικός τόπος του σημείου Ρ κατά τη διπλή αυτή κίνηση καλείται σπείρα του Αρχιμήδη, με εξίσωση σε πολικές συντεταγμένες ΟΡ=αθ.
4) Τετραγωνίζουσα του Ιππία (4ος αιώνας π.Χ.)
Θεωρούμε ένα τετράγωνο ΟΑΓΔ .Αν το τμήμα ΔΓ αρχίσει να κινείται προς τα κάτω με σταθερή ταχύτητα μένοντας παράλληλο προς το ΟΑ και ταυτόχρονα το ΟΔ να περιστρέφεται γύρω από το Ο με σταθερή ταχύτητα επίσης, και τα δύο τμήματα φθάσουν ταυτόχρονα στην ΟΑ, τότε τα σημεία τομής τους θα γράψουν μία καμπύλη. Η καμπύλη αυτή είναι η τετραγωνίζουσα .
Θεωρούμε την ημιευθεία ΟΒ, η οποία μπορεί να περιστρέφεται του σταθερού σημείου Ο. Πάνω σε αυτήν κινείται σημείο Ρ με σταθερή ταχύτητα από το Ο προς το Β. Ο γεωμετρικός τόπος του σημείου Ρ κατά τη διπλή αυτή κίνηση καλείται σπείρα του Αρχιμήδη, με εξίσωση σε πολικές συντεταγμένες ΟΡ=αθ.
4) Τετραγωνίζουσα του Ιππία (4ος αιώνας π.Χ.)
Θεωρούμε ένα τετράγωνο ΟΑΓΔ .Αν το τμήμα ΔΓ αρχίσει να κινείται προς τα κάτω με σταθερή ταχύτητα μένοντας παράλληλο προς το ΟΑ και ταυτόχρονα το ΟΔ να περιστρέφεται γύρω από το Ο με σταθερή ταχύτητα επίσης, και τα δύο τμήματα φθάσουν ταυτόχρονα στην ΟΑ, τότε τα σημεία τομής τους θα γράψουν μία καμπύλη. Η καμπύλη αυτή είναι η τετραγωνίζουσα .
Και οι γνωστές μας κωνικές τομές (Μαθηματικά κατεύθυνσης Β΄Λυκείου)
(x-a)2(x2+y2) = b2x2
(x2+y2) = b