Οι αριθμοί Fibonacci
Ποιος ήταν ο Fibonacci
Ο Fibonacci ήταν πολύ γνωστός στην εποχή του και αναγνωρίζεται σήμερα ως ο μεγαλύτερος μαθηματικός του Μεσαίωνα. Γεννήθηκε στην Πίζα τη δεκαετία του 1170 και πέθανε αυτή του 1240. Το όνομά του έχει δοθεί σε δύο δρόμους, στην Πίζα και στη Φλωρεντία. Το πραγματικό του όνομα ήταν Leonardo Pisano, όμως ο ίδιος αποκαλούσε τον εαυτό του Fibonacci, σύντμηση του Filius Bonacci (υιός του Bonacci), από το όνομα του πατέρα του.
Στον μαθηματικό κλάδο είναι γνωστός για τη συμβολή του στον διαφορικό και ολοκληρωτικό λογισμό και για τους αριθμούς του που, όπως θα δούμε, είναι μία ακολουθία αριθμών για τους οποίους η φύση παρουσιάζει ιδιαίτερη προτίμηση, γεγονός που ακόμα και σήμερα δεν είναι πλήρως κατανοητό.
Το πρόβλημα με τα κουνέλια
Το πρόβλημα που μελέτησε και τον οδήγησε μάλλον τυχαία στον ορισμό της ακολουθίας του, αφορούσε την αναπαραγωγή κουνελιών. Το έθεσε στο ιστορικό βιβλίο του Liber Abaci(βιβλίο των υπολογισμών) που δημοσιεύθηκε για πρώτη φορά το 1202.
Το πρόβλημα έχει ως εξής:
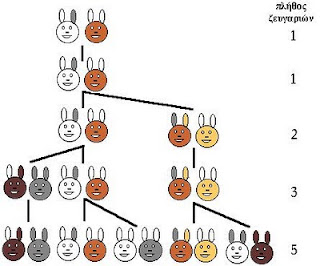
Σε ένα σπίτι στο χωριό γεννιέται ένα ζευγάρι κουνέλια. Τα κουνέλια αυτά χρειάζονται 2 μήνες για να μεγαλώσουν και να αρχίσουν να γεννούν. Έτσι μετά από δύο μήνες το ζευγάρι αυτό γεννά ένα νέο ζευγάρι στην αρχή κάθε μήνα. Τα νέα ζευγάρια μεγαλώνουν και αναπαράγονται κι αυτά με τον ίδιο τρόπο. Πόσα ζευγάρια κουνέλια θα έχουμε μετά από 3 μήνες , 4 μήνες , 6 μήνες , μετά από ένα χρόνο;
Απάντηση:
Στην αρχή του πρώτου μήνα έχουμε 1 ζευγάρι κουνέλια
Στην αρχή του δεύτερου μήνα έχουμε πάλι ένα ζευγάρι
Στην αρχή του τρίτου μήνα το ζευγάρι γεννά και έχουμε 2 ζευγάρια
Στην αρχή του τέταρτου μήνα το πρώτο ζευγάρι γεννά πάλι , αλλά το δεύτερο δεν είναι σε θέση ακόμη, δηλαδή 3 ζευγάρια.
Στην αρχή του πέμπτου μήνα γεννά πάλι το αρχικό ζευγάρι , γεννά και το δεύτερο , δε γεννά το τρίτο. Σύνολο 5 ζευγάρια
Στην αρχή του πέμπτου μήνα γεννά πάλι το αρχικό ζευγάρι , γεννά και το δεύτερο , δε γεννά το τρίτο. Σύνολο 5 ζευγάρια
Έτσι, το πλήθος των ζευγαριών των κουνελιών στην αρχή κάθε μήνα είναι 1, 1, 2, 3, 5, 8, 13, 21, 34, .. Παρατηρήστε ότι κάθε αριθμός στην ακολουθία είναι το άθροισμα των δύο προηγούμενων. Αυτό είναι λογικό να συμβαίνει μια και στην αρχή κάθε μήνα έχουμε τα ζευγάρια που είχαμε τον προηγούμενο μήνα και επιπλέον τόσα νεογέννητα ζευγάρια όσα και ενήλικα ζευγάρια γονέων έχουμε.
Άρα οι αριθμοί Fibonacci είναι: 1,1,2,3,5,8,13,21,34,55,89,..... με τον κάθε αριθμό να προκύπτει από το άθροισμα των δύο προηγούμενων του.
1+1=2 , 1+2=3 , 3+5=8 , 5+8=13 ,.....
Οι αριθμοί Fibonacci και ο χρυσός λόγος φ
Η δεύτερη και σημαντικότερη ιδιότητα των αριθμών αυτών είναι η εξής:
Αν διαιρέσουμε κάθε αριθμό με τον επόμενό του , τότε οι λόγοι που θα βρούμε τείνουν να προσεγγίσουν τον άρρητο αριθμό 0,618... , το γνωστό χρυσό αριθμό που διεθνώς συμβολίζεται με το ελληνικό γράμμα φ.
Δείτε μερικά παραδείγματα:
8:13=0,615..
13:21=0,619.
21:34=0,6176..
34:55=0,61818.. και όσο συνεχίζουμε τόσο πιο κοντά στον αριθμό φ βρισκόμαστε.
Ο αριθμός φ δεν ήταν άγνωστος στους αρχαίους Έλληνες. Ο Πυθαγόρας ήταν από τους πρώτους που παρατήρησε ότι τα φυτά και τα ζώα δεν μεγαλώνουν τυχαία , αλλά με ακριβείς μαθηματικούς κανόνες.
Τα σχέδια των λουλουδιών , η ανάπτυξη των φύλλων γύρω από το μίσχο , η ανάπτυξη των βελόνων στα έλατα κ.α. ακολουθούν τις προηγούμενες ακολουθίες. Χρησιμοποιήθηκε στην αρχιτεκτονική (Παρθενώνας) , στη ζωγραφική (Μόνα Λίζα) με τα γνωστά τέλεια αποτελέσματα. Τους αριθμούς Fibonacci τους συναντάμε επίσης στο ανθρώπινο χέρι (κάθε άνθρωπος έχει 2 χέρια, κάθε ένα από τα οποία έχει 5 δάχτυλα, κάθε δάκτυλο αποτελείται από 3 τμήματα που χωρίζονται από 2 αρθρώσεις) , στο ανθρώπινο πρόσωπο , στη δομή του D.N.A. και ίσως σχεδόν παντού στη φύση)