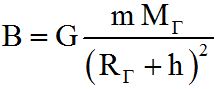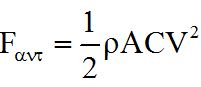Άλμα εις μήκος και παγκόσμια ρεκόρ. Μαθηματικά μοντέλα και φυσική.

 

Το άλμα εις μήκος θεωρείται ένα από τα πιο σημαντικά και θεαματικότερα αγωνίσματα του κλασικού αθλητισμού και τις πρώτες αναφορές για αυτό τις βρίσκουμε στην αρχαιότητα, με διαφορετική όμως μορφή από την σημερινή. 

Η διαδικασία ήταν η ίδια, ενώ κάποιες διαφορές υπήρχαν στον τρόπο που πραγματοποιούσαν τα άλματα και που μετρούσαν τις επιδόσεις. Ο βατήρας των αρχαίων Ελλήνων ήταν μια πλίθινη πλάκα και το σημείο προσγείωσης το σημείωναν χαράζοντας μια γραμμή. Ο αθλητής πηδούσε ψηλά και μακριά και στη συνέχεια προσγειωνόταν με τα πόδια ενωμένα, χωρίς να πέφτει κάτω. Ευρήματα για τις επιδόσεις τους δεν έχουν βρεθεί, καθώς έδιναν περισσότερη σημασία στην τεχνική και λιγότερο στην επίδοση.

Σαν αγώνισμα καθιερώθηκε από τους Άγγλους το 1336, ενώ οι Έλληνες το συμπεριέλαβαν στο πρόγραμμα των Ολυμπιακών Αγώνων του 1896, με πρώτη καταγεγραμμένη επίδοση τα 6,10 μέτρα.

Το άλμα εις μήκος έχει αναλυθεί σε πολλές μελέτες τα τελευταία χρόνια με χρήση μαθηματικών μοντέλων και έχουν συγκεντρωθεί πολλές πληροφορίες για τους παράγοντες που επηρεάζουν την τελική επίδοση. 

Ως πιο σημαντικός παράγοντας φαίνεται να είναι η συσχέτιση ανάμεσα στην ταχύτητα και στο πόσο μακριά εκτινάσσεται ο αθλητής. Με βάση μια έρευνα του 2005 στην Αγγλία και χρησιμοποιώντας ειδικά φωτοκύτταρα σε διάφορα σημεία του διαδρόμου, φάνηκε ότι η οριζόντια ταχύτητα μπορεί να χρησιμοποιηθεί για να κερδηθεί κατακόρυφη ταχύτητα και κατά συνέπεια η τελική επίδοση να είναι μεγαλύτερη.

Εκτός όμως από την τεχνική και την ταχύτητα του αθλητή, σημαντικό ρόλο παίζουν και τα σωματικά χαρακτηριστικά των αθλητών. Στα μαθηματικά μοντέλα που χρησιμοποιήθηκαν, φάνηκε πως αθλητές με τραπεζοειδείς ωμοπλάτες και μεγαλύτερο εύρος κίνησης στην ωμική ζώνη, είχαν μικρότερη μέση και καλύτερες επιδόσεις. 

Οι υψηλόσωμοι επίσης αθλητές ευνοούνται, λόγω του κέντρου βάρους του σώματος που βρίσκεται σε υψηλότερο σημείο, ενώ και η αναλογία μεταξύ εύρους των ώμων και της λεκάνης ασκεί σημαντική επίδραση, με τις γυναίκες που έχουν ανδρική σωματική διάπλαση να πετυχαίνουν καλύτερες επιδόσεις από τις υπόλοιπες.

Στην παραπάνω φωτογραφία βλέπουμε τον Bob Beamon να αγωνίζεται στο άλμα εις μήκος, τον Οκτώβριο του 1968 στους Ολυμπιακούς Αγώνες στο Μεξικό.

Το εκπληκτικό του άλμα στα 8,90 μέτρα οδήγησε στην άποψη ότι η απίστευτη αυτή επίδοση οφειλόταν στο υψόμετρο που βρίσκεται η πόλη του Μεξικό (σχεδόν 2.300 μέτρα από την επιφάνεια της θάλασσας). Ας μην ξεχνάμε ότι το ρεκόρ αυτό καταρρίφθηκε 21 χρόνια μετά, στο παγκόσμιο πρωτάθλημα στίβου στο Τόκιο το 1991, αρχικά από τον Carl Lewis με άλμα 8,91 και στη συνέχεια από τον Mike Powell που απάντησε με άλμα στα 8,95 μέτρα. 

Στο υψόμετρο αυτό η δύναμη του βάρους είναι μικρότερη σε σχέση με το βάρος στην επιφάνεια της θάλασσας, όπως και η πυκνότητα του αέρα.

Στο έγκυρο site physicsgg.me (φυσικοί και φυσική από το διαδίκτυο) διαβάζουμε κατά πόσο οι δύο αυτοί παράγοντες βοήθησαν στην επίτευξη αυτού του εξωπραγματικού ρεκόρ.

Ας δούμε αρχικά την επίδραση της βαρύτητας. 

Το βάρος Β ενός σώματος μάζας m εξαρτάται από το ύψος h της επιφάνειας της Γης με βάση τον τύπο:

 

όπου G η σταθερά της παγκόσμιας έλξης.

 

Στην πόλη του Μεξικό που βρίσκεται για την ακρίβεια 2.240 μέτρα από την επιφάνεια της θάλασσας και έπειτα από αριθμητικούς υπολογισμούς, υπολογίζεται ότι το βάρος ενός σώματος μειώνεται κατά 99,225% σε σχέση με το βάρος του στην επιφάνεια της θάλασσας. 

Με άλλα λόγια η μείωση του βάρους δεν μπορεί να κάνει τη διαφορά.

Τι γίνεται όμως με την πυκνότητα του αέρα;

 

Μια δύναμη που μπορεί να επηρεάσει τον άλτη του μήκους είναι η δύναμη της αντίστασης του αέρα, η οποία μπορεί να υπολογιστεί από τον τύπο:

 

όπου V η ταχύτητα του σώματος, Α και C παράμετροι που εξαρτώνται από το σχήμα και το μέγεθος του σώματος και ρ η πυκνότητα του αέρα.

Η πυκνότητα του αέρα μειώνεται καθώς αυξάνεται το υψόμετρο, αλλά η εξάρτησή της από το ύψος είναι δύσκολο να μοντελοποιηθεί. Παίζουν ρόλο η πίεση και η θερμοκρασία ακόμα, μεγέθη που εξαρτώνται από τις καιρικές συνθήκες.

Μπορεί όμως αυτή η ελάττωση της πυκνότητας να δημιουργήσει ένα παγκόσμιο ρεκόρ στο άλμα εις μήκος;

 

Η κίνηση ενός σώματος που κινείται στον αέρα δεν είναι τόσο απλό πρόβλημα και ένας τρόπος να λυθεί το ζήτημα αυτό είναι να αντληθούν δεδομένα από το βίντεο του άλματος και να χρησιμοποιηθούν στην αριθμητική επίλυση του προβλήματος.

 

 

 

Μελετώντας το άλμα μπορούμε να υπολογίσουμε τον χρόνο πτήσης του αθλητή, το μέγιστο ύψος από την επιφάνεια του εδάφους και την αρχική του ταχύτητα.

Με χρήση αριθμητικών υπολογισμών δημιουργήθηκε η παρακάτω εικόνα που δείχνει τις γραφικές παραστάσεις της κατακόρυφης θέσης συναρτήσει της οριζόντιας θέσης. Αυτές αντιστοιχούν σε τρεις περιπτώσεις, σύμφωνα με το μαθηματικό μοντέλο αριθμητικής προσέγγισης που χρησιμοποιήθηκε. Η μπλε γραμμή αντιστοιχεί σε άλμα στην επιφάνεια της θάλασσας, χωρίς αέρα. Η κόκκινη αντιστοιχεί σε άλμα στην πόλη του Μεξικού και η πράσινη σε άλμα στην επιφάνεια της θάλασσας με αέρα.

 

Παρατηρούμε ότι υπάρχει μια μικρή διαφορά.

Το μοντέλο με την αντίσταση στο επίπεδο της θάλασσας δίνει άλμα 8,89 μέτρων, ενώ στην πόλη του Μεξικού, με αέρα, δίνει άλμα 8,96 μέτρων, μια απόκλιση δηλαδή 7 εκατοστών. Καμία σχέση όμως με την αύξηση του ρεκόρ κατά 55 εκατοστά που πέτυχε ο Beamon. 

Συνεπώς το τεράστιο κατόρθωμα του δεν οφειλόταν, ούτε στη μικρότερη δύναμη της βαρύτητας, ούτε στην μικρότερη πυκνότητα του αέρα, αλλά κατά 99,9% στις δυνάμεις του ίδιου του αθλητή και σε 0,1% στους ευνοϊκούς παράγοντες των νόμων της Φυσικής.